Pitch Shift
Description
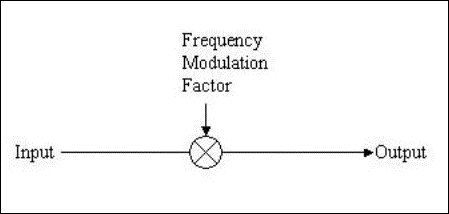
As the name implies, the
pitch shift algorithm modulates the frequency of the input signal by a
designated interval. Csound has built-in opcodes to raise and lower pitches by
user-specified intervals. The pitch is scaled proportionally and the time is
scaled inverse proportionally according to a frequency modulation factor. This
factor designates how the original input signal samples will be arranged in the
output signal. A factor of 2 will cause the frequency of the signal to be
doubled and the number of samples to be cut in half (i.e. every other sample is
discarded).
Graphical Depiction
Effect Formula
|
y[n] = f(x[n]) |
|
y[n] = output
signal |
|
x[n] = input
signal |
|
f() = frequency
modulation function |
Source Code
(.csd files can be viewed with Notepad or any text
editor)
Example Audio Clips
|
Original Unprocessed
Signal |
|
|
Raised half step |
|
|
Raised whole step |
|
|
Raised minor third |
|
|
Raised major third |
|
|
Raised perfect fourth |
|
|
Raised diminished fifth |
|
|
Raised perfect fifth |
|
|
Raised minor sixth |
|
|
Raised major sixth |
|
|
Raised minor seventh |
|
|
Raised major seventh |
|
|
Raised one octave |
References
Lehman, Scott
(1996). Effects Explained. Harmony Central. Retrieved 6/04 from
http://www.harmony-central.com/Effects/effects-explained.html
Mikelson, Hans
(2000). Modeling a multieffects processor in Csound. In Boulanger,
Richard (2000), The Csound book (pp 575-594). Cambridge, MA: MIT Press.
Schindler,
Allan. (1998). Eastman Csound tutorial.
Eastman School of Music. Retrieved 6/04 from
http://www.esm.rochester.edu/onlinedocs/allan.cs/
Vercoe, Barry.
(1992). The public Csound reference manual, version 4.16. MIT
Press. Retrieved 6/04 from http://www.lakewoodsound.com/csound/hypertext/manual.htm
Zolzer, Udo.
(2002). Digital audio effects. West Sussex, England: Baffins Lane.