Reverb
Description
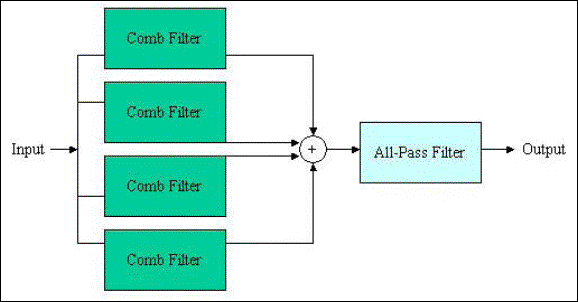
Digital reverb attempts to
simulate the timbre of natural sounds as they reflect off of different surfaces
in different sized and shaped rooms. Digitally implementing this effect is
complicated, requiring a series of filters, delays, and sound dampening
algorithms. Applying reverb to an audio signal requires a large amount of
memory and processing time. Fortunately, a reverb opcode is built into csound.
It is built using comb filters and all pass filters. This opcode requires three
parameters - input signal, reverb time, and decay factor. The reverb time
designates how long the reverberation will last. The decay factor designates as
a percentage how much faster lower frequencies will decay than higher
frequencies.
Graphical
Depiction
Effect
Formula
|
y[n] = x[n] +
f(x[n], t, d) |
|
y[n] = output
signal |
|
x[n] = input
signal |
|
f(x[n], t, d) =
reverberation function |
|
t = reverb time
(sec) |
|
d = decay factor
[0,1] |
Source
Code
(.csd files can be viewed with Notepad or any text
editor)
Example Audio
Clips
|
Original Unprocessed
Signal |
|
|
Reverb with 3 second
reverb time and .5 decay |
|
|
Reverb with 2.5 second
reverb time and .7 decay |
|
|
Reverb with 1.5 second
reverb time and 0 decay |
References
Lehman, Scott
(1996). Effects Explained. Harmony Central. Retrieved 6/04 from
http://www.harmony-central.com/Effects/effects-explained.html
Mikelson, Hans
(2000). Modeling a multieffects processor in Csound. In Boulanger,
Richard (2000), The Csound book (pp 575-594). Cambridge, MA: MIT Press.
Schindler,
Allan. (1998). Eastman Csound tutorial.
Eastman School of Music. Retrieved 6/04 from
http://www.esm.rochester.edu/onlinedocs/allan.cs/
Vercoe, Barry.
(1992). The public Csound reference manual, version 4.16. MIT
Press. Retrieved 6/04 from http://www.lakewoodsound.com/csound/hypertext/manual.htm
Zolzer, Udo.
(2002). Digital audio effects. West Sussex, England: Baffins Lane.